Thermodynamics and Propulsion

17. Convective Heat Transfer

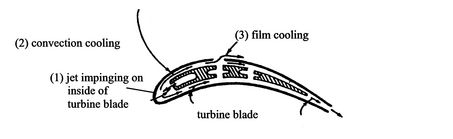
The second type of heat transfer to be examined is convection, where a key problem is determining the boundary conditions at a surface exposed to a flowing fluid. An example is the wall temperature in a turbine blade because turbine temperatures are critical for creep (and thus blade) life. A view of the problem is given in Figure 17.1, which shows a cross-sectional view of a turbine blade. There are three different types of cooling indicated, all meant to ensure that the metal is kept at a temperature much lower than that of the combustor exit flow in which the turbine blade operates. In this case, the turbine wall temperature is not known and must be found as part of the solution to the problem.

Figure 17.1: Turbine blade heat transfer configuration (from Aircraft Engines and Gas Turbines, Kerrebrock, J.L.)

Figure 17.2: Temperature and velocity distributions near a surface

To find the turbine wall temperature, we need to analyze convective heat transfer, which means we need to examine some features of the fluid motion near a surface. The conditions near a surface are illustrated schematically in Figure 17.2. In a region of thickness $\delta'$ , there is a thin ``film'' of slowly moving fluid through which most of the temperature difference occurs. Outside this layer, $T$ is roughly uniform (this defines $\delta'$ ). The heat flux can thus be expressed as

$$\dot{q} = \frac{\dot{Q}}{A} = \frac{k(T_w - T_\infty)}{\delta'}.$$ (17..1)

It cannot be emphasized enough that this is a very crude picture. The general concept, however, is correct, in that close to the wall, there is a thin layer in which heat is transferred basically by conduction. Outside of this region is high mixing. The difficulty is that the thickness of the layer is not a fluid property. It depends on velocity (Reynolds number), structure of the wall surface, pressure gradient and Mach number. Generally $\delta'$ is not known and needs to be found and it is customary to calculate the heat transfer using $k_\textrm{fluid} / \delta'$ . This quantity has the symbol $h$ and is known as the convective heat transfer coefficient. The units of $h$ are W/m²K. The convective heat transfer coefficient is defined by

$$\dot{q} = \frac{\dot{Q}}{A} = h(T_w - T_\infty).$$ (17..2)

Equation (17.2) is often called Newton's Law of Cooling. For many situations of practical interest, the quantity $h$ is still known mainly through experiments.

Muddy Points

How do we know that $\delta'$ is not a fluid property? (MP 17.1)