Thermodynamics and Propulsion

6.9 Muddiest Points on Chapter 6

MP 6..1   So, do we lose the capability to do work when we have an irreversible process and entropy increases?

Absolutely. We will see this in a more general fashion very soon. The idea of lost work is one way to view what ``entropy is all about.''

MP 6..2   Why do we study cycles starting with the Carnot cycle? Is it because it is easier to work with?

Carnot cycles are the best we can do in terms of efficiency. We use the Carnot cycle as a standard against which all other cycles are compared. We will see in class that we can break down a general cycle into many small Carnot cycles. Doing this we can gain insight in which direction the design of efficient cycles should go.

MP 6..3   How does one interpret h-s diagrams?

I find $h$ -$s$ diagrams useful, especially in dealing with propulsion systems, because the difference in stagnation $h$ can be related (from the Steady Flow Energy Equation) to shaft work and heat input. For processes that just have shaft work (compressors or turbines) the change in stagnation enthalpy is the shaft work. For processes that just have heat addition or rejection at constant pressure, the change in stagnation enthalpy is the heat addition or rejection.

MP 6..4   Is it always OK to ``switch'' T-s and h-s diagrams?

No! This is only permissible for perfect gases with constant specific heats. We will see, when we examine cycles with liquid-vapor mixtures, that the $h$ -$s$ diagrams and the $T$ -$s$ diagrams look different.

MP 6..5   What is the best way to become comfortable with T-s diagrams?

I think working with these diagrams may be the most useful way to achieve this objective. In doing this, the utility of using these coordinates (or $h$ -$s$ coordinates) should also become clearer. I find that I am more comfortable with $T$ -$s$ or $h$ -$s$ diagrams than with $P$ -$v$ diagrams, especially the latter because it conveys several aspects of interest to propulsion engineers: work produced or absorbed, heat produced or absorbed, and loss.

MP 6..6   What is a reversible adiabat physically?

Let's pick an example process involving a chamber filled with a compressible gas and a piston. We assume that the chamber is insulated (so no heat transfer to or from the chamber) and the process is thus adiabatic. Let us also assume that the piston is ideal, such that there is no friction between the walls of the chamber and the piston. The gas is at some temperature $T_1$ . We now push the piston in and compress the gas. The internal energy of the system will then increase by the amount of work we put in and the gas will heat up and be at higher pressure. If we now let the piston expand again, it will return to its original position (no friction, ideal piston) and the work we took from the environment will be returned (we get the exact same amount of work back and leave no mark on the environment). Also, the temperature and the pressure of the gas return to the initial values. We thus have an adiabatic reversible process. For both compression and expansion we have no change in entropy of the system because there is no heat transfer and also no irreversibility. If we now draw this process in the $h$ -$s$ or $T$ -$s$ diagram we get a vertical line since the entropy stays constant: $S = \textrm{constant}$ or $\Delta S=0$ and we can also call this process an isentropic process.

MP 6..7   If there is an ideal efficiency for all cycles, is there a maximum work or maximum power for all cycles?

Yes. As with the Brayton cycle example, we could find the maximum as a function of the appropriate design parameters.

MP 6..8   Do we ever see an absolute variable for entropy? So far, we have worked with deltas only.

It is probably too strong a statement to say that for ``us'' the changes in entropy are what matters, but this has been my experience for the type of problems aerospace engineers work on. Some values of absolute entropy are given in Table A.8 in SB&VW. We will also see, in the lectures on Rankine cycles, that the entropy of liquid water at a temperature of $0.01^\circ \textrm{C}$ and a pressure of $0.6113 \textrm{ kPa}$ has been specified as zero for problems involving two-phase (steam and water) behavior.

MP 6..9   I am confused as to $dS = dQ_\textrm{rev}/T$ as opposed to $dS \geq dQ_\textrm{rev}/T$ .

Both of these are true and both can always be used. The first is the definition of entropy. The second is a statement of how the entropy behaves. Section 6.5 attempts to make the relationship clearer through the development of the equality $dS = dQ/T + dW_\textrm{lost}/T$ .

MP 6..10   For irreversible processes, how can we calculate $dS$ if not equal to $dQ/T$ ?

We need to define a reversible process between the two states in order to calculate the entropy (see MP 6.9). See VN Chapter 5 (especially) for discussion of entropy or Section 6.5. If you are still in difficulty, come and see me.

MP 6..11   Is $\Delta S$ path dependent?

No. Entropy is a function of state (see Gibbs) and thus $\Delta S$ is path independent. For example we could have three different paths connecting the same two states and therefore have the same change in entropy

$$\Delta S_\textrm{path I} = \Delta S_\textrm{path II} = \Delta S_\textrm{path III}.$$

MP 6..12   Are $Q_\textrm{rev}$ and $W_\textrm{rev}$ the $Q$ and $W$ going from the final state back to the initial state?

Yes. We have an irreversible process from state 1 to state 2. We then used a reversible process to restore the initial state 1 (we had to do work on the system and extract heat from the system).

MP 6..13   Why do we find stagnation enthalpy if the velocity never equals zero in the flow?

The stagnation enthalpy (or stagnation temperature) is a useful reference quantity. Unlike the static temperature it does not vary along a streamline in an adiabatic flow, even if irreversible. It was thus the natural reference temperature to use in describing the throttling process. In addition, changes in stagnation enthalpy (or stagnation temperature) are direct representations of the shaft work or heat associated with a fluid component. The static enthalpy is not, unless we assume that changes in $KE$ are small. Measurement of stagnation temperature thus allows direct assessment of shaft work in a turbine or compressor, for example.

MP 6..14   Why does $T_t$ remain constant for throttling?

Because for a steady adiabatic flow with no shaft work done the Steady Flow Energy Equation yields constant stagnation enthalpy even though the flow processes might not be reversible (see notes). For a perfect gas with constant specific heats, $h_t =c_p T_t$ , thus the stagnation temperature remains constant.

MP 6..15   How do you tell the difference between shaft work/power and flow work in a turbine, both conceptually and mathematically?

Let us look at the expansion of a flow through a turbine using both the control mass approach and the control volume approach. Using the control mass approach we can model the situation by tracking $1\textrm{ kg}$ of air as follows: state 1 -- before the expansion we have $1\textrm{ kg}$ of air upstream of the turbine. We then push the gas into the turbine and expand it through the blade rows. After the expansion we take $1\textrm{ kg}$ of air out of the turbine and the mass of air is downstream of the turbine -- state 2. The work done by the gas is work done by the turbine (blades moved around by the gas) plus the work done by pressures (flow work). Using the first law we can then write for the change of internal energy of $1\textrm{ kg}$ of air:

$$u_2 - u_1 = - w_\textrm{shaft} + p_1v_1 - p_2v_2\qquad \textrm{(adiabatic turbine: $dq = 0$)}.$$

When entering the turbine, the fluid has to push the surroundings out of the way to make room for itself (it has volume $v_1$ and is at $p_1$ ) -- the work to do this is $+p_1v_1$ . When leaving the turbine the fluid is giving up room and the work to keep that volume $v_2$ at pressure $p_2$ is freed; thus $-p_2v_2$ . We can then write for the shaft work

$$w_\textrm{shaft} = u_1 + p_1v_1 - (u_2 + p_2v_2).$$

The right hand side of the above equation is the change in enthalpy $(h_1 - h_2)$ . This is another example to show how useful enthalpy is (enthalpy is the total energy of a fluid: the internal energy plus the extra energy that it is credited with by having a volume $v$ at pressure $p$ ). The shaft work output by the turbine is equal to the change in enthalpy (enthalpy contains the flow work!).

$$w_\textrm{shaft} = h_1 - h_2.$$

We can also solve this problem by using the 1^st law in general form (control volume approach):

$$\frac{dE_{CV}}{dt}=\sum\dot{Q}_{CV}+\sum\dot{W}_{shaft}+\sum\dot{W}_{shear} +\sum\dot{W}_{piston}+\sum_i\dot{m}_i(h_i+\frac{c_i^2}{2}+gz).$$

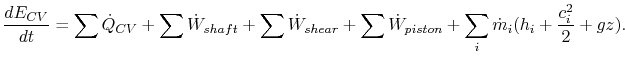
Note that in this form the flow work is buried in $h$ already! For this turbine, we can drop the unsteady term on the left and neglect heat fluxes (adiabatic turbine), shear work and piston work (no pistons but blades, so we keep the shaft work). Further we assume that changes in potential energy and kinetic energy are negligible and we obtain for $1\textrm{ kg/s}$ air

$$0 = -w_\textrm{shaft} + h_1 - h_2.$$

We obtain the same result as before: $w_\textrm{shaft} = h_1 - h_2$ .

MP 6..16   Is the entropy change in the equations two lines above the total entropy change? If so, why does it say $\Delta S_\textrm{atm}$ ?

The entropy change in question is the entropy change due to the heat produced by friction only.

$$(\Delta S_\textrm{atm})_{\textrm{due to frictional work \emph{onl... ...textrm{atm}} =\frac{(W_\textrm{system} - W_\textrm{received})}{T_\textrm{atm}}.$$

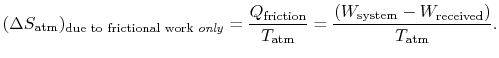
MP 6..17   Why does $\Delta S_\textrm{irrev}=\Delta S_\textrm{total}$ ?

When we wrote this equality, we were considering a system that was returned to its original state, so that there were no changes in any of the system properties. All evidence of irreversibility thus resides in the surroundings.

MP 6..18   In discussing the terms ``closed system'' and ``isolated system,'' can you assume that you are discussing a cycle or not?

The terms closed system and isolated system have no connection to whether we are discussing a cycle or not. They are attributes of a system (any system), whether undergoing cyclic behavior, one-way transitions, or just sitting there.

MP 6..19   Does a cycle process have to have $\Delta S=0$ ?

Entropy is a state function. If the process is cyclic, initial and final states are the same. So, for a cyclic process, $\Delta S=0$ .

MP 6..20   In a real heat engine, with friction and losses, why is $\Delta S=0$ still if $TdS=dQ+d\Phi$ ?

The change in entropy during a real cycle is zero because we are considering a complete cycle (returning to initial state) and entropy is a function of state (holds for both ideal and real cycles!). Thus if we integrate $dS = dQ/T + d\Phi/T$ around the real cycle we will obtain $\Delta S_\textrm{cycle} = 0$ . What essentially happens is that all irreversibilities ($d\Phi$ 's) are turned into additional heat that is rejected to the environment. The amount of heat rejected in the real ideal cycle $Q_R^\textrm{real}$ is going to be larger than the amount of heat rejected in an ideal cycle $Q_R^\textrm{ideal}$ :

$$\nonumber Q_R^\textrm{ideal} = Q_A \frac{T_R}{T_A} \textrm{(from $\Delta S_\textrm{cycle} = 0$)}$$

$$Q_R^\textrm{real} = Q_A\frac{T_R}{T_A} + T_R \Delta S_\Phi \textrm{(from $\Delta S_\textrm{cycle} = 0$)}.$$

We will see this better using the $T$ -$s$ diagram. The change of entropy of the surroundings (heat reservoirs) is $\Delta S_\textrm{surr} = -Q_A/T_A + Q_R^\textrm{real}/T_R = \Delta S_\Phi > 0$ . So $\Delta S_\textrm{cycle} = 0$ even for real cycles, but $\Delta S_\textrm{total} = \Delta S_\textrm{cycle} + \Delta S_\textrm{surr} = \Delta S_\Phi > 0$ .

MP 6..21   Is it safe to say that entropy is the tendency for a system to go into disorder?

Entropy can be given this interpretation from a statistical perspective, and this provides a different and insightful view of this property. At the level in which we have engaged the concept, however, we focus on the macroscopic properties of systems, and there is no need to address the idea of order and disorder; as we will see, entropy is connected to the loss of our ability to do work, and that is sufficient to make it a concept of great utility for the evaluation and design of engineering systems. We will look at this in a later lecture. If you are interested in pursuing this, places to start might be Great Ideas in Physics by Lightman (paperback book by an MIT professor), or Modern Thermodynamics by Kondepudi and Prigogine.