The list of the 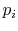 is a precise description of the randomness in
the system, but the number of quantum states in almost any
industrial system is so high this list is not useable. We thus look
for a single quantity, which is a function of the
is a precise description of the randomness in
the system, but the number of quantum states in almost any
industrial system is so high this list is not useable. We thus look
for a single quantity, which is a function of the 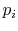 , that gives
an appropriate measure of the randomness of a system. As shown
below, the entropy provides this measure.
, that gives
an appropriate measure of the randomness of a system. As shown
below, the entropy provides this measure.
There are several attributes that the desired function should have.
The first is that the average of the function over all of the
microstates should have an extensive behavior. In other words the
microscopic description of the entropy of a system 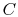 , composed of
parts
, composed of
parts 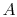 and
and 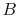 should be given by
should be given by
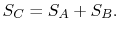 |
(7..4) |
Second is that entropy should increase with randomness and should be
largest for a given energy when all the quantum states are
equiprobable.
The average of the function over all the microstates is defined by
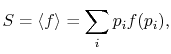 |
(7..5) |
where the function 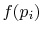 is to be found. Suppose that system
is to be found. Suppose that system 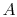 has
has 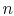 microstates and system
microstates and system 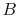 has
has 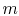 microstates. The
entropies of systems
microstates. The
entropies of systems 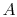 ,
, 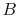 , and
, and 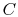 , are defined by
, are defined by
In Equations (7.5) and
(7.6), the term 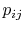 means the probability
of a microstate in which system
means the probability
of a microstate in which system 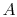 is in state
is in state 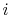 and system
and system 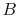 is in state
is in state 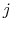 . For Equation (7.4) to hold
given the expressions in Equations (7.6),
. For Equation (7.4) to hold
given the expressions in Equations (7.6),
The function 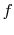 must be such that this is true regardless of the
values of the probabilities
must be such that this is true regardless of the
values of the probabilities 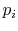 and
and 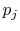 . This will occur if
. This will occur if
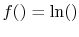 because
because
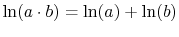 .
.
To verify this, make this substitution in the expression for 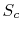 in the first part of Equation (7.6c)
(assume the probabilities
in the first part of Equation (7.6c)
(assume the probabilities 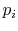 and
and 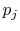 are independent, such that
are independent, such that
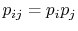 , and split the log term):
, and split the log term):
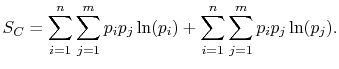 |
(7..8) |
Rearranging the sums, (7.8) becomes
![$\displaystyle S_C = \sum_{i=1}^n\left\{p_i\ln(p_i)\left[\sum_{j=1}^m p_j\right]\right\}+ \sum_{j=1}^m\left\{ p_j\ln(p_j)\left[\sum_{i=1}^n p_i\right]\right\}.$](img923.png) |
(7..9) |
Because
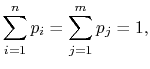 |
(7..10) |
the square brackets in the right hand side of Equation
(7.9) can be set equal to unity, with the result written as
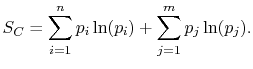 |
(7..11) |
This reveals the top line of Equation
(7.7) to be the same as the bottom line, for any 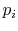 ,
, 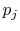 ,
, 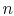 ,
,
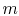 , provided that
, provided that 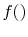 is a logarithmic function. Reynolds and
Perkins show that the most general
is a logarithmic function. Reynolds and
Perkins show that the most general 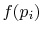 is
is
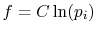 ,
where
,
where 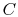 is an arbitrary constant. Because the
is an arbitrary constant. Because the 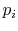 are less than
unity, the constant is chosen to be negative to make the entropy
positive.
are less than
unity, the constant is chosen to be negative to make the entropy
positive.
Based on the above, a statistical definition of entropy can be given
as:
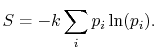 |
(7..12) |
The constant 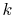 is known as the Boltzmann constant,
is known as the Boltzmann constant,
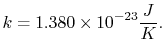 |
(7..13) |
The value of 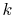 is (another wonderful result!) given by
is (another wonderful result!) given by
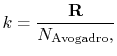 |
(7..14) |
where
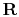 is the universal gas constant,
is the universal gas constant,
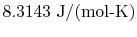 and
and
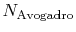 is Avogadro's number,
is Avogadro's number,
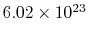 molecules per mol. Sometimes
molecules per mol. Sometimes 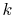 is called the
gas constant per molecule. With this value for
is called the
gas constant per molecule. With this value for 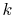 , the statistical
definition of entropy is identical with the macroscopic definition
of entropy.
, the statistical
definition of entropy is identical with the macroscopic definition
of entropy.
UnifiedTP
|

